Eksplorasi Kubus: Geometri Dimensi Tiga

Geometri dimensi tiga, atau stereometri, merupakan cabang matematika yang mempelajari objek-objek dalam ruang tiga dimensi. Salah satu bangun ruang paling fundamental dan sering ditemui adalah kubus. Kubus, dengan sifat-sifatnya yang seragam dan simetris, menjadi dasar penting untuk memahami konsep-konsep yang lebih kompleks dalam stereometri. Bagi siswa kelas 12, pemahaman mendalam tentang kubus tidak hanya relevan untuk ujian sekolah, tetapi juga untuk aplikasi praktis dalam berbagai bidang seperti arsitektur, teknik, dan desain.

Artikel ini akan mengupas tuntas tentang kubus, mulai dari definisi, sifat-sifatnya, hingga bagaimana menghitung berbagai elemen penting seperti panjang diagonal dan luas permukaan. Kita juga akan menyajikan beberapa soal latihan beserta pembahasannya yang dirancang khusus untuk siswa kelas 12, membantu memperkuat pemahaman dan kesiapan dalam menghadapi tantangan soal-soal geometri.

I. Definisi dan Sifat-Sifat Kubus

Kubus adalah bangun ruang yang dibatasi oleh enam buah persegi yang kongruen (memiliki ukuran dan bentuk yang sama). Setiap persegi ini berperan sebagai sisi atau muka kubus. Keistimewaan kubus terletak pada kesederhanaan dan keseragamannya.

Mari kita jabarkan sifat-sifat utama kubus:

• Sisi: Kubus memiliki 6 buah sisi yang semuanya berbentuk persegi dan kongruen.
• Rusuk: Kubus memiliki 12 buah rusuk yang memiliki panjang yang sama. Rusuk adalah garis-garis perpotongan antara dua sisi.
• Titik Sudut: Kubus memiliki 8 buah titik sudut. Titik sudut adalah pertemuan antara tiga buah rusuk.
• Sudut Antar Rusuk: Setiap sudut yang dibentuk oleh dua rusuk yang bertemu pada satu titik sudut adalah sudut siku-siku (90 derajat).
• Sudut Antar Sisi: Sudut yang dibentuk oleh dua sisi yang berpotongan adalah sudut siku-siku (90 derajat).
• Diagonal Sisi: Kubus memiliki 12 buah diagonal sisi. Diagonal sisi adalah garis yang menghubungkan dua titik sudut yang berhadapan pada satu sisi. Panjang diagonal sisi pada kubus dengan panjang rusuk ‘a’ adalah $asqrt2$.
• Diagonal Ruang: Kubus memiliki 4 buah diagonal ruang. Diagonal ruang adalah garis yang menghubungkan dua titik sudut yang berhadapan tetapi tidak terletak pada satu sisi. Panjang diagonal ruang pada kubus dengan panjang rusuk ‘a’ adalah $asqrt3$.

II. Rumus-Rumus Penting pada Kubus

Memahami sifat-sifat kubus akan memudahkan kita dalam menghafal dan menerapkan rumus-rumus berikut. Misalkan ‘a’ adalah panjang rusuk kubus.

• Luas Permukaan Kubus: Luas permukaan adalah jumlah luas dari keenam sisinya. Karena setiap sisi adalah persegi dengan luas $a^2$, maka:
  Luas Permukaan = $6 times (textluas satu sisi)$
  Luas Permukaan = $6a^2$

• Volume Kubus: Volume adalah ruang yang ditempati oleh kubus.
  Volume = $(textpanjang rusuk)^3$
  Volume = $a^3$

• Panjang Diagonal Sisi: Seperti yang disebutkan sebelumnya, diagonal sisi dapat dihitung menggunakan teorema Pythagoras pada salah satu sisi persegi.
  Diagonal Sisi = $sqrta^2 + a^2 = sqrt2a^2 = asqrt2$

• Panjang Diagonal Ruang: Diagonal ruang dapat dihitung dengan menerapkan teorema Pythagoras dua kali. Bayangkan sebuah segitiga siku-siku yang dibentuk oleh satu rusuk, satu diagonal sisi, dan satu diagonal ruang.
  Diagonal Ruang = $sqrt(textdiagonal sisi)^2 + a^2$
  Diagonal Ruang = $sqrt(asqrt2)^2 + a^2$
  Diagonal Ruang = $sqrt2a^2 + a^2$
  Diagonal Ruang = $sqrt3a^2$
  Diagonal Ruang = $asqrt3$

III. Soal dan Pembahasan

Mari kita terapkan konsep-konsep di atas melalui beberapa contoh soal yang sering muncul dalam konteks pembelajaran kelas 12.

Soal 1:

Sebuah kubus memiliki panjang rusuk 8 cm. Hitunglah:
a. Luas permukaan kubus.
b. Volume kubus.
c. Panjang diagonal sisi kubus.
d. Panjang diagonal ruang kubus.

Pembahasan Soal 1:

Diketahui panjang rusuk kubus, $a = 8$ cm.

a. Luas Permukaan Kubus:
Luas Permukaan = $6a^2$
Luas Permukaan = $6 times (8 text cm)^2$
Luas Permukaan = $6 times 64 text cm^2$
Luas Permukaan = $384 text cm^2$

b. Volume Kubus:
Volume = $a^3$
Volume = $(8 text cm)^3$
Volume = $512 text cm^3$

c. Panjang Diagonal Sisi Kubus:
Diagonal Sisi = $asqrt2$
Diagonal Sisi = $8sqrt2$ cm

d. Panjang Diagonal Ruang Kubus:
Diagonal Ruang = $asqrt3$
Diagonal Ruang = $8sqrt3$ cm

Soal 2:

Volume sebuah kubus adalah 125 cm³. Tentukan panjang rusuk kubus tersebut.

Pembahasan Soal 2:

Diketahui Volume kubus = 125 cm³.
Rumus volume kubus adalah $V = a^3$.
Maka, $a^3 = 125 text cm^3$.
Untuk mencari panjang rusuk ‘a’, kita perlu mencari akar pangkat tiga dari 125.
$a = sqrt125 text cm^3$
$a = 5 text cm$
Jadi, panjang rusuk kubus tersebut adalah 5 cm.

Soal 3:

Panjang diagonal ruang sebuah kubus adalah $6sqrt3$ cm. Hitunglah luas permukaan kubus tersebut.

Pembahasan Soal 3:

Diketahui panjang diagonal ruang = $6sqrt3$ cm.
Rumus diagonal ruang kubus adalah $d_ruang = asqrt3$.
Maka, $asqrt3 = 6sqrt3$ cm.
Dengan membandingkan kedua sisi, kita dapatkan panjang rusuk $a = 6$ cm.

Selanjutnya, kita hitung luas permukaan kubus:
Luas Permukaan = $6a^2$
Luas Permukaan = $6 times (6 text cm)^2$
Luas Permukaan = $6 times 36 text cm^2$
Luas Permukaan = $216 text cm^2$
Jadi, luas permukaan kubus tersebut adalah 216 cm².

Soal 4:

Sebuah kubus memiliki panjang diagonal sisi 10 cm. Tentukan volume kubus tersebut.

Pembahasan Soal 4:

Diketahui panjang diagonal sisi = 10 cm.
Rumus diagonal sisi kubus adalah $d_sisi = asqrt2$.
Maka, $asqrt2 = 10$ cm.
Untuk mencari panjang rusuk ‘a’, kita bagi kedua sisi dengan $sqrt2$:
$a = frac10sqrt2$ cm.
Untuk merasionalkan penyebut, kita kalikan pembilang dan penyebut dengan $sqrt2$:
$a = frac10sqrt22$ cm
$a = 5sqrt2$ cm.

Sekarang kita hitung volume kubus:
Volume = $a^3$
Volume = $(5sqrt2 text cm)^3$
Volume = $(5^3) times (sqrt2)^3 text cm^3$
Volume = $125 times (2sqrt2) text cm^3$
Volume = $250sqrt2$ cm³
Jadi, volume kubus tersebut adalah $250sqrt2$ cm³.

Soal 5:

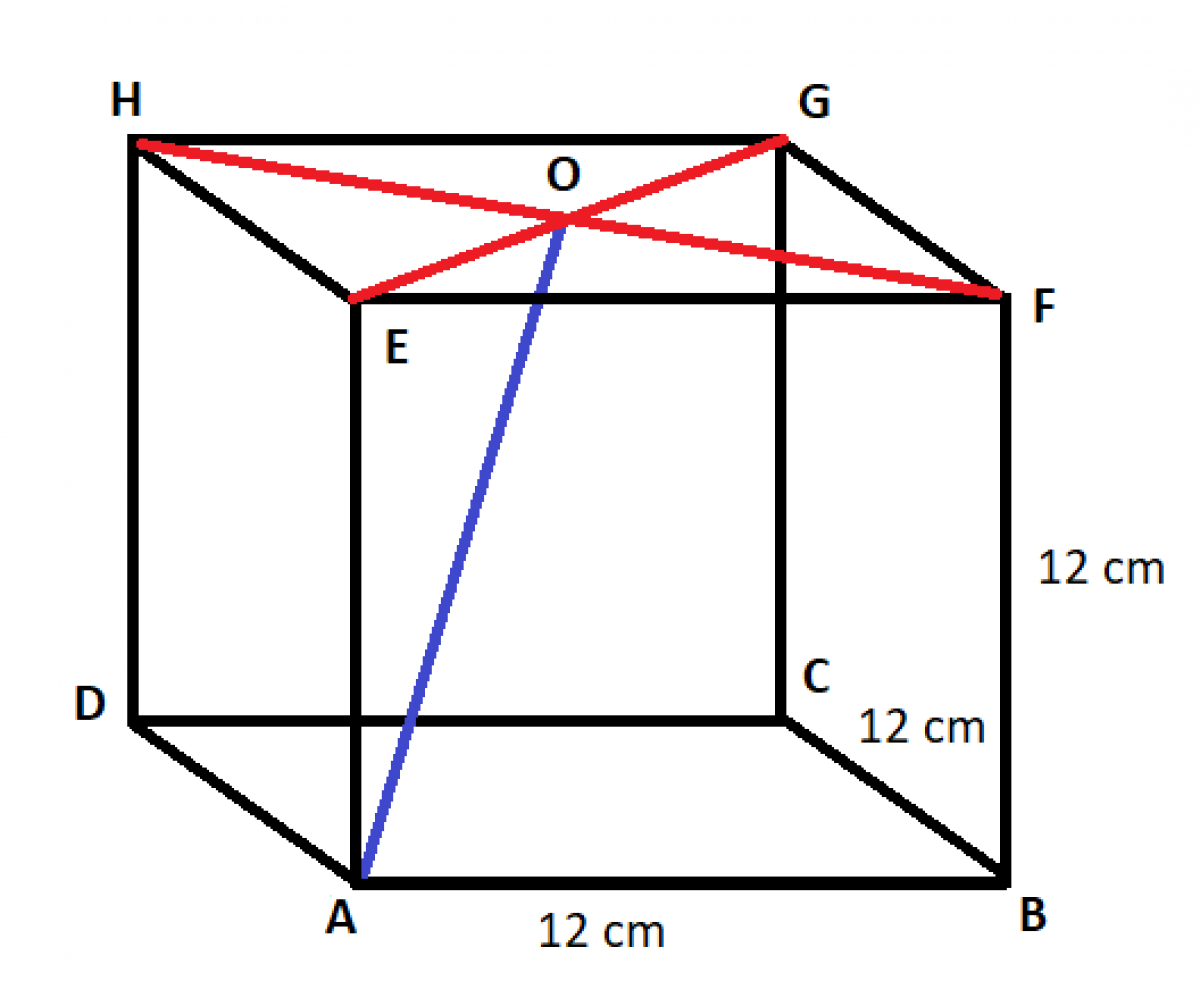
Perhatikan kubus ABCD.EFGH, di mana A adalah titik sudut di bagian bawah depan kiri, dan E adalah titik sudut di bagian atas depan kiri. Jika panjang rusuk kubus adalah 12 cm, tentukan jarak antara titik A dan titik G.

Pembahasan Soal 5:

Titik A adalah salah satu titik sudut pada alas kubus, misalnya di koordinat (0,0,0). Titik G adalah titik sudut yang berhadapan secara diagonal di bagian atas belakang kanan, misalnya di koordinat (12,12,12). Jarak antara titik A dan titik G adalah panjang diagonal ruang kubus.

Diketahui panjang rusuk kubus, $a = 12$ cm.
Jarak antara titik A dan titik G adalah panjang diagonal ruang kubus.
Rumus diagonal ruang kubus adalah $druang = asqrt3$.
$druang = 12sqrt3$ cm.

Alternatif menggunakan koordinat:
Titik A dapat diasumsikan berada di (0,0,0).
Titik G akan berada di (12,12,12).
Jarak antara dua titik $(x_1, y_1, z_1)$ dan $(x_2, y_2, z_2)$ adalah $sqrt(x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2$.
Jarak A ke G = $sqrt(12-0)^2 + (12-0)^2 + (12-0)^2$
Jarak A ke G = $sqrt12^2 + 12^2 + 12^2$
Jarak A ke G = $sqrt144 + 144 + 144$
Jarak A ke G = $sqrt3 times 144$
Jarak A ke G = $sqrt3 times sqrt144$
Jarak A ke G = $sqrt3 times 12$
Jarak A ke G = $12sqrt3$ cm.

IV. Kesimpulan

Kubus, sebagai bangun ruang dimensi tiga yang paling dasar, menawarkan banyak konsep menarik untuk dieksplorasi. Memahami sifat-sifatnya yang konsisten dan menguasai rumus-rumus terkait luas permukaan, volume, diagonal sisi, dan diagonal ruang adalah kunci keberhasilan dalam mengerjakan soal-soal stereometri.

Melalui soal dan pembahasan yang telah disajikan, diharapkan siswa kelas 12 dapat memperdalam pemahaman mereka tentang kubus. Latihan yang konsisten akan membangun kepercayaan diri dan kemampuan untuk menerapkan prinsip-prinsip geometri dalam berbagai situasi. Ingatlah bahwa geometri bukanlah sekadar menghafal rumus, melainkan memahami logika di baliknya dan bagaimana menggunakannya secara efektif. Teruslah berlatih dan jangan ragu untuk menjelajahi lebih jauh dunia dimensi tiga yang menakjubkan ini.